莱布尼茨、二进制和伏羲卦图
发布者:生活中的数据分析发布时间:2021-03-17浏览次数:2326
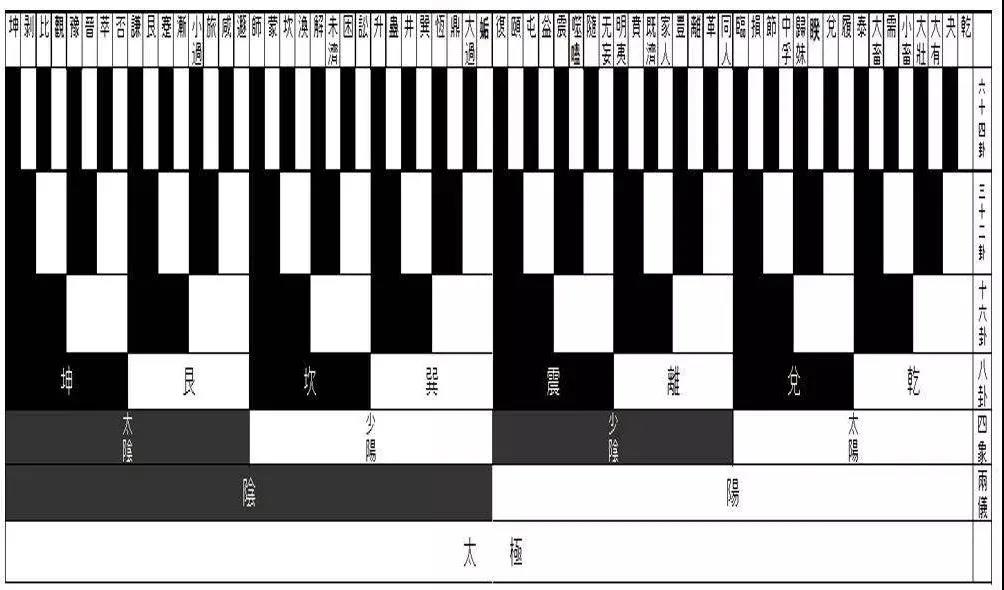
殷商时期,中国已经有了比较完备的十进制计数法。根据人类文明发展史的常识,《周易》作为一部文明源头的著作,其内容和思想都处于文化的萌芽状态,书中的算术知识极为简单,根本没有二进制的内容。通读《周易》可知,所谓算术知识,无非也只是计数而已,那都是采用十进制表述的。易学里的伏羲卦图种类很多,有八卦图,也有六十四卦图。八卦图的排序一般具有对称性,六十四卦图则是根据卜筮之辞排序的。通行的《周易》和从长沙马王堆汉墓出土的帛书《周易》的排序不尽相同,但是,都没有按照二进制的序数排列。易学研究领域有一种说法,阴爻和阳爻具有数字特征。从殷商出土的一些陶器、甲骨和竹简上留存的信息得知,阴爻是从偶数演变而来,阳爻是从奇数演变而来。这些符号形成以后,虽然凸显了其中的哲学意义,也残存了数字的模糊影像,因此,数学家们把《易经》和数学扯上了关系。始作俑者是魏晋时期的刘徽,他在《九章算术注》中写道:“昔者包牺氏始画八卦,以通神明之德,以类万物之情,作九九之数,以合六爻之变。”包牺氏是伏羲的别名。刘徽的观点影响了之后的数学家。北宋的秦九韶在《数书九章》中说:数学“爰自河图洛书,闿发秘奥,八卦九畴,错综精微,极而至于大衍皇极之用。”明朝的程大位在《算法统宗》中载有伏羲作卦图的插画,书中写道:“数何肇?其肇自图书乎!伏羲得之以画卦,大禹得之以序畴,列圣得之以开物成务。凡天官、地员、律历、兵赋以及纤悉杪忽,莫不有数,则莫不本于《易》。”邵雍利用象数推演替代哲学思考,给人的感觉像在进行数学运算。他在《观物外篇》论述道:“有意必有言,有言必有象,有象必有数。数立则象生,象生则言著彰,言著彰则意显。象数则筌蹄也。”意思是说,思想可以用语言表达,语言可以用图象表达,图象可以用数字表达。反之亦然。所以,象数是表达思想的工具。这与莱布尼茨“通用字符”的思想颇为一致。在邵雍绘制的先天图中,只要把阴爻当作0,把阳爻当作1,其排列与二进制的序数完全相同,这无疑是一个二进制的模型。但是,这个二进制的模型只是无心插柳柳成荫的结果,不能据此认为邵雍创立了二进制,只能说是数学思想把先天图统一到了二进制的理论系统之中。数学发展史的常识告诉我们,任何一项数学成就的取得,无外乎两个原因,一是数学内部理论研究的进展,二是数学外部社会发展进步的要求。首先,邵雍并不是数学家,他在数学上没有任何建树,没有撰写过数学论著,也未见他与哪一个数学家有过学术交往。邵雍没有任何论述二进制的片言只语,他也根本不通晓二进制理论,他既没有明确界定和命名二进制的数学概念,也没有科学地表述二进制的重要性质和意义,更没有完善二进制与其它数学概念之间的逻辑关系。从邵雍的论著里,也看不出他具有超出常人的数学素养,邵雍创立二进制就像当今的“民科数学家”要解决哥德巴赫猜想一样,是绝对做不到的。不要说他,就是与他同时代的数学家们,也没有人涉猎过二进制的研究领域。卦图符号在《周易》里早已存在,宋代之前,《周易》和伏羲卦图中根本没有二进制的信息。邵雍在先天图里将这些符号重新进行排序,并不是主动按照二进制原理做的,只是碰巧排出了二进制数的顺序而已。所以,我们只能谨慎地说,先天图里生长着二进制的萌芽。有人提出,邵雍说的“加一倍法”就是“逢二进一”法则,这完全是毫无根据的猜测。仅从词义上理解,它们也不是同一件事情。“加一倍法”是增加了一倍的意思,即乘以2,是指伏羲卦图的生成过程,上一层级的每一卦顺次增加一爻,则卦的个数将增加一倍。即“一分为二,二分为四,四分为八,八分为十六,十六分为三十二,三十二分为六十四。故曰分阴分阳,迭用柔刚,易六位而成章也4。”这完全是十进制的说法,跟二进制的“逢二进一”没有任何关系。从概念的原本意义考察,由阳爻和阴爻组成的卦图符号表示的是抽象的哲学事物,即使它们与数字有联系,也是十进制中的1—64,包括邵雍在内的宋元明清的易学家和数学家,没有一个人提出,可以用二进制数来表达。邵雍在绘制先天图的过程中,凡涉及到计数问题,都是用十进制去解决的。如说到八卦的排序,他的表述是:乾一、兑二、离三、震四、巽五、坎六、艮七、坤八。如果邵雍懂得二进制原理,那么卦图符号的顺序就会很清晰,不需要借助任何方法,就很容易被人记忆,但是,直到南宋,朱熹还根据八卦符号的直观形象编写了记忆口诀:乾三连(☰),坤六断(☷),震仰盂(☳),艮覆碗(☶),离中虚(☲),坎中满(☵),兑上缺(☱),巽下短(☴)。这从一个侧面反映出邵雍和朱熹都没有意识到先天图与二进制之间的密切关系。清朝乾嘉年间,有一位著名的数学家汪莱,他的《参两算经》是专门论述进位制理论的著作,他也没有指出先天图就是二进制。那么,先天图怎么恰巧就与二进制的序数相同的呢?这个问题困惑了许多人,甚至有学者用概率论的方法解读认为,64个元素总共有64!种排列方法,要在这天文数字的排列中找到与二进制数的顺序完全相同的一个,这几乎就是不可能事件啊!进而得出,如果邵雍不是熟知二进制原理,他怎么就能够找到这一个排列呢?其实,先天图和二进制都是由两个基本符号表示的,这其实就是元素可重复排列的组合问题。从2种符号中每次取3个,排成一排,共有23=8种排法,得到《周易》里的八卦和二进制里的前八个数。从2种符号中每次取6个,排成一排,共有26=64种排法,得到《周易》里的六十四卦和二进制里的前六十四个数。先天图中的卦序与二进制的序数相同,其实是一个必然事件。邵雍并不需要懂得二进制知识,二进制不是绘制先天图的必要条件。事实是邵雍创造性地运用了另外一个数学方法,用“树图”自然而然地生成了一棵二进制的“数学树”,这就是《伏羲六十四卦次序图》。
莱布尼茨1703年5月18日致白晋的信中提到,他在二十多年前就发明了二进制,那正是他在巴黎创立微积分的时期。莱布尼茨在1707年12月15日致布尔盖(D.Bourguet)的信中提到:“当初我创立二进制算术时,对《易经》的卦图并不是很了解。”莱布尼茨有一份手稿《二进制算术的阐释》,写作时间是1679年3月15日,一直没有发表,被搁置了二十多年。但凡数学上的创新和发现,都是循着前人开辟的道路进行的,在超越前人的过程中,并不能保证可以眷顾到所有具有启迪性的思想成果。莱布尼茨在发明二进制之前,只是从卫匡国的《中国上古史》和斯比塞尔的《中国文史评析》上间接地了解《易经》,这些文献都不是数学著作,虽然卫匡国称《易经》是数学著作,也只是一种臆测。莱布尼茨所见到的伏羲卦图不是邵雍绘制的先天图,卦图的顺序是按照哲学理念排列的,没有按照二进制的顺序排列。莱布尼茨的学术兴趣是发展“通用字符”的思想,他关心的是卦图符号的语言和逻辑意义,压根儿没有从数学角度去考虑问题,所以,莱布尼茨在易学文献中无从获悉二进制的信息。如果莱布尼茨在见到伏羲卦图时就受到启发,他的二进制论文早就提前二十多年就发表了。另外,有人说斯比塞尔著作中在介绍伏羲卦图时提到的短语“binarium multiplicatis”是二进制的意思,莱布尼茨由此受到启发。这是不顾历史事实的臆测。斯比塞尔写作这部著作的时候,二进制的概念还没有被明确提出。“二进制”一词是被莱布尼茨引入学术界的,当时,他还没有思考二进制的问题。斯比塞尔不是数学家,他无从知道什么是二进制。这个短语也不是二进制的意思,而是指2的乘方,是说伏羲卦图产生的方式。其实,莱布尼茨发现二进制的契机很简单,完全就是水到渠成,一蹴而就的结果。从数学认知的规律考虑,具备数学基本素养的人只要熟悉了进位制理论,提出任何进位制都是平凡的推论。事实上,任何一个比1大的自然数都可以作为一种进位制的基数,理论上可以构造出无穷多种进位制,这在数学上是一个极为简单的常识。莱布尼茨1663年暑假去到耶拿大学学习数学,老师是魏格留斯(Erhard Weigel)教授。魏格留斯对古希腊的数学思想研究颇有心得,崇尚毕达哥拉斯和柏拉图的数学观,认为物质世界的和谐符合数学法则。莱布尼茨深受老师思想的启迪。1672年,魏格留斯在耶拿大学的学刊《Joham Meyer》上发表了《圣十结构》一文,系统地提出了四进制的概念,用0、1、2、3来表示所有的数,“满三进一”,象征着“三”是完满。不久,莱布尼茨写出《二进制算术的阐释》手稿。毫无疑问,莱布尼茨无论是从老师的课堂上或者从老师的论文里,熟知进位制理论是没有疑义的。从莱布尼茨的《论中国人的自然哲学》中我们知道,莱布尼茨非常熟悉进位制的历史,他提到,古罗马人曾经使用混合五进制和十进制的算术,提到历史上出现过四进制和十二进制,他明确地写道:正是魏格留斯的四进制,“给了我一个机会,提出一切数都可以用二进制的0和1写出。”由此可知,莱布尼茨发明二进制是受到他老师的启发,与伏羲卦图没有关系。有人诟病莱布尼茨,质疑他有意掩饰受到伏羲卦图启发而发现二进制,是没有事实依据的。莱布尼茨从来没有把二进制的发明权据为己有。他反而大力吹捧是伏羲早在他四千年前就发明了二进制,他还把这个重大发现归功于白晋。事实上,各种进位制的计数方式早已存在于人类的社会活动之中了。在世界文明的发源地,古巴比伦人第一个发明了位值制,使用过六十进制,玛雅人使用过二十进制,中国独自发明了位值制,是最早使用十进制的。商代甲骨卜辞中就有了1—9的数码和位值制的记数法,战国时期出现了十进制的筹算记数,以空代表0,非常先进。太平洋上的芒阿雷瓦岛的部落早在1450年之前就在使用二进制,至今,波利尼西亚和澳大利亚的有些土著居民还在使用二进制5,其实,数学家的所谓发明,也就是把人类世俗生活中的计数方法进行了数学化的处理,所以,发明二进制谈不上是什么了不起的数学成果。其实与莱布尼茨同时代的数学家洛布克威兹(Y.Lobkowitz)在1670年出版的《双面数学》中,也有讨论十二进制和二进制的内容。莱布尼茨也许不知道,在莎士比亚那个时代,英国有一位才华横溢的数学家哈里奥特6(Thomas Harriot),他遗存的手稿里有大量数学和物理原创性的成果。因为当时没有科学类期刊,这些成果无处发表。哈里奥特1603年的手稿《数学计算与注解》中,就有详细论述二进制算术的内容,理论结构几乎与莱布尼茨的相同,用0和1作为基本计数符号,命名二进制为Binary numeration,提出了加减法以及乘法运算法则,还讨论了用连分数的形式表示二进制的相关问题。
注:摘自《莱布尼茨、二进制和伏羲卦图》作者:张小平 江辉 马宏云


